Fast Fourier Transform

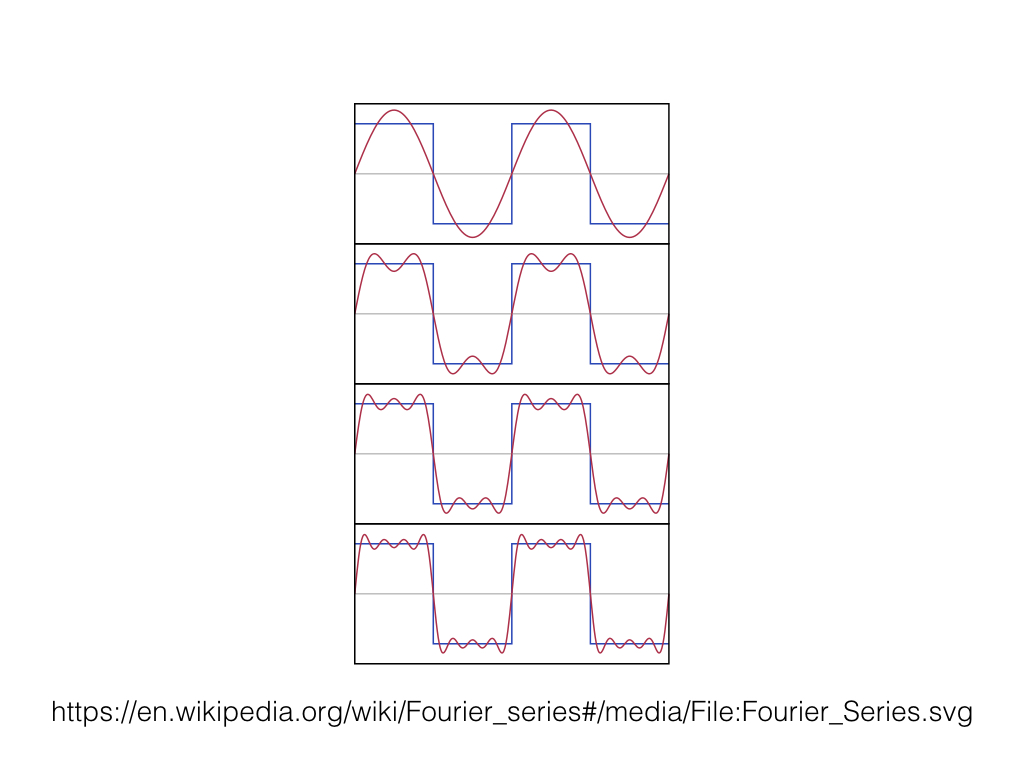
Every sound breaks down into a collection of sine waves, each with its own frequency, amplitude, and phase. This is the Fourier theorem.

Normally, we represent our audio signal as amplitude over time.

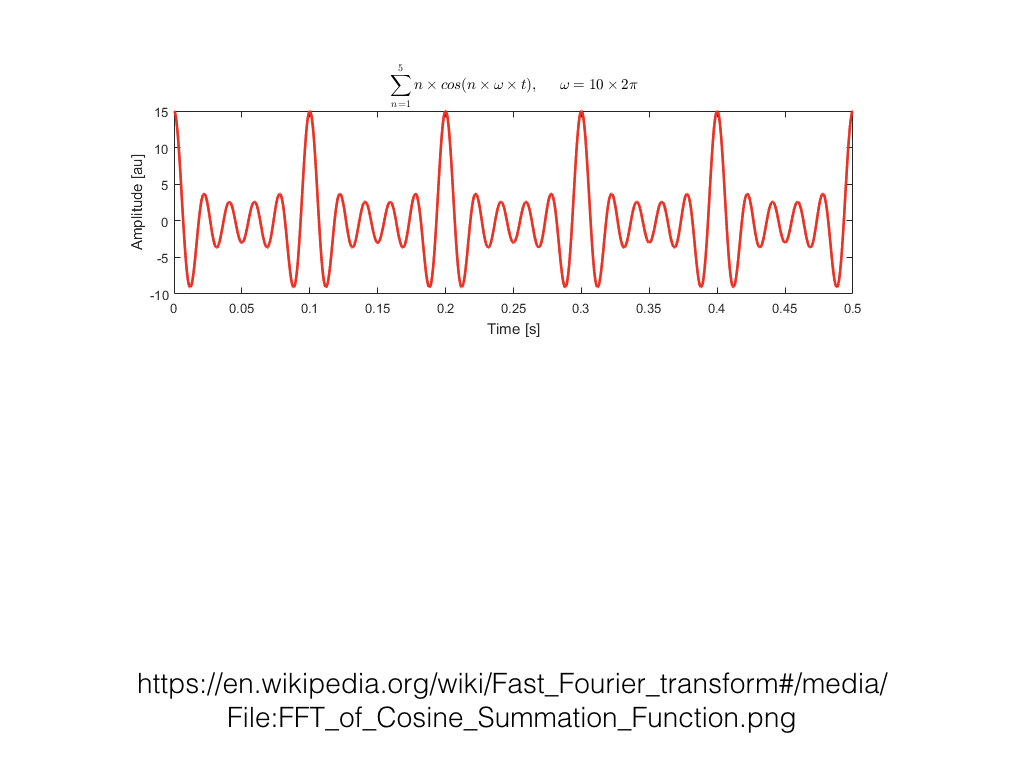
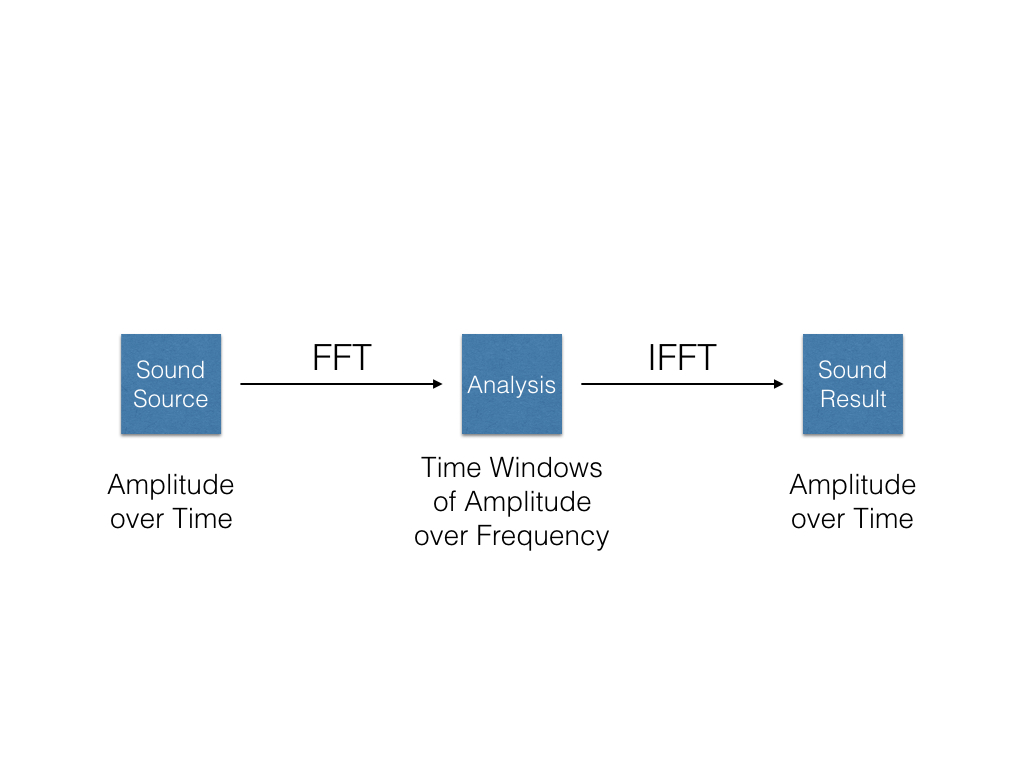
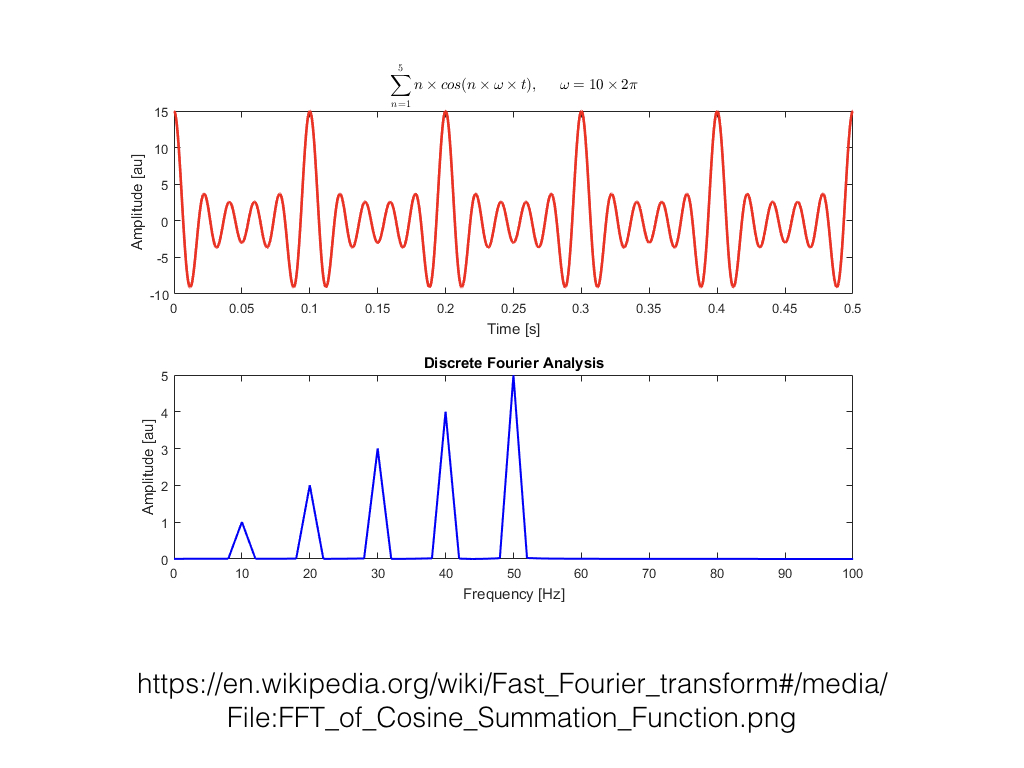
Sometimes, we'd like the frequency information as well. A Fast Fourier Transform, or FFT, breaks down a sound into its component parts. So instead of amplitude over time, we have a series of windows, each with amplitude over frequency. An Inverse Fast Fourier Transform, or IFFT, takes the component parts and puts them back together.

For a specified range in time, we can change our representation from amplitude over time to amplitude over frequency. We call each of these ranges a "window". A window is usually short, usually 0 to 20ms. A series of windows gives us time, amplitude, and frequency. However, we lose some information with each window. We must decide whether we want more accurate duration or more accurate frequency information. Short windows provide accurate duration but poor frequency. Long windows provide accurate frequency but poor duration.

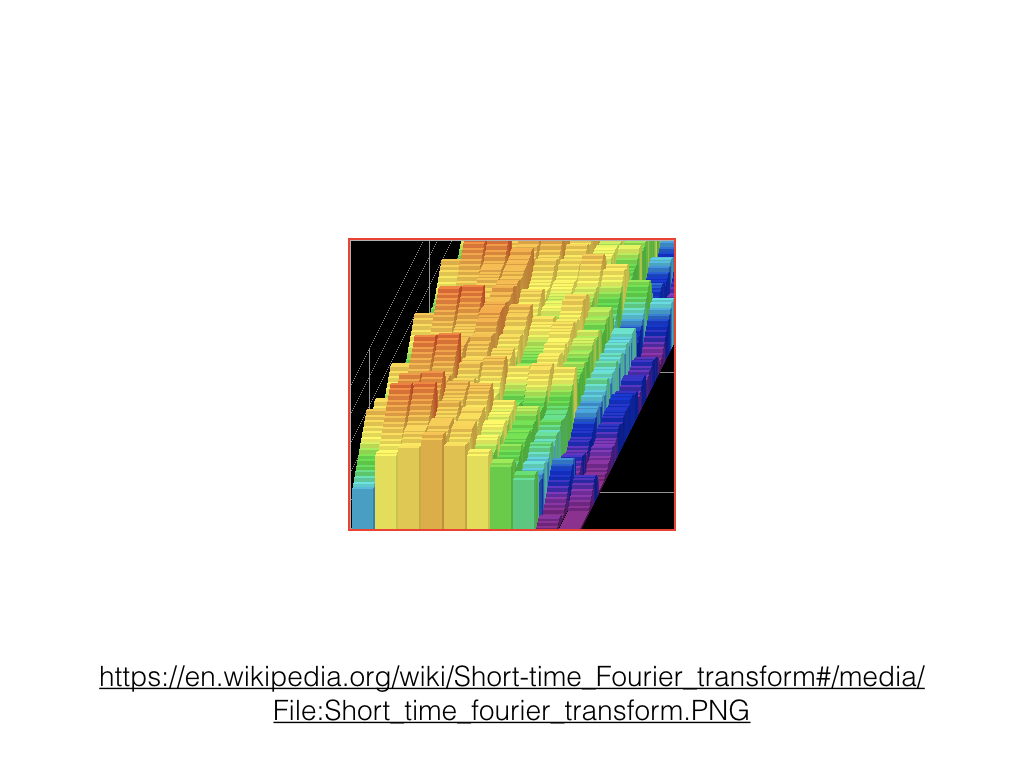
So what's so great about the Fast Fourier Transform? First off, we can use FFT to analyze a sound source. We can determine the fundamental frequency of a given sound source. We can detect changes in the frequency content over time.

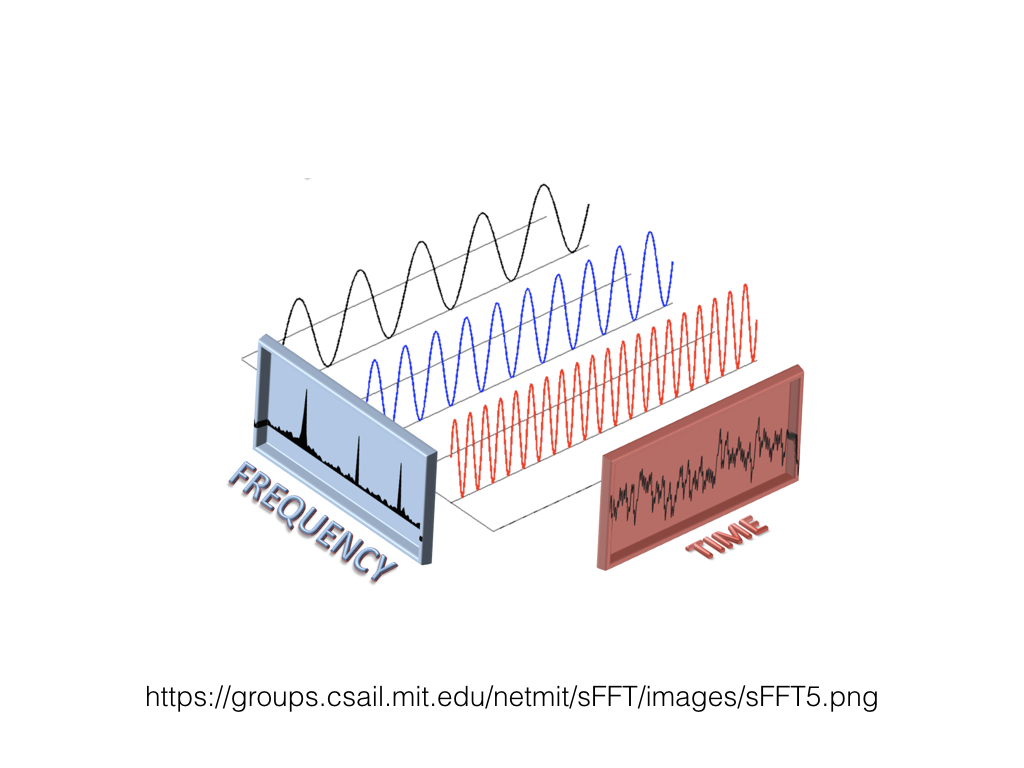
We can also change the result of the FFT analysis. Then, we apply an Inverse FFT on the analysis to result in changes of the frequency content of the sound. For example, filters often use FFT. Think of autotune. Morphing of sounds. Compressing audio file size by eliminating unheard frequencies. The applications are truly endless.